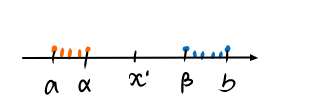Recall: Riemann 和的局限
- 两个任意难以满足: 难满足
- 因此 需要尽量大/小 (不一定是端点)
一、函数的可积性
Darboux 和
设 在 有界, 其上,下确界为 . 振幅
设 是 的分割, 记
称 及
分别为 在分割 下的Darboux上和及下和/大和及小和
为振幅
- 与介点集无关, 和介于 ,
- 分割 :
引理1:加细分割
设 是分割 添加 个分点的加细分割,则
- 加细分割具有 上和减小,下和增加 性
- 而且“减少/增加不了多少”:是受控的,受控于
Proof
只需证明的情形假设分割加入分割则放缩且在上确界
引理2
设 和 是 的任意两分割,则
Proof
令共同加细则
- 为的分割 为非空上有界集
- 为的分割 为非空下有界集
上、下积分
称为 的下积分
上、下积分与 Darboux 上、下和的关系
结论:
Proof
取则最小上界特殊上界
Darboux 定理
设 在 有界,则
Analysis
分析(1)的情况
即显然即证Proof
根据定义(最小上界)分割使得取可能为分割令则为与的共同加细则为至多添加个分点得到此处回代得到具体值而显然
可积/第I充要条件
设 在 有界, 则
- 应用:Dirichelet 函数不可积:
Proof
已知: 有:
让 尽可能大,并不影响左右,取上确界
取sup:
即:
根据 #Darboux定理
已知: :
有:
夹逼性:
又
推论
设 在 有界,则
因此弱化成如下
可积/第II充要条件
设 在 有界,则
分割
Proof
由推论可证(弱化)
已知
因此
由 #可积/第I充要条件 即证
几何意义:零面积集

用任意小的矩形能够盖住函数 (零面积集)
要使 :
- 或者 很小
- 或者虽 不小,但其对应的小区间长度和很小
- 若 小: 可满足
- 若 做不到小:通常是有间断点
=> 概念: 测度
设 在 有界, 则其振幅
Analysis
用 定义的两个要素即可
Proof
令
即证:
有根据定义使得
二、可积函数及性质证明
闭区间连续→可积
Proof
由 及 #Cantor定理 知:
即 且 有
取分割 满足 ,则分割中 , 有
故
闭区间有界+有限间断→可积
若 在 有界, 且仅有限个间断点, 则
符号说明: 代表 关于 的分点的指标求和
不妨设 仅有一个间断点 :(不是分点)
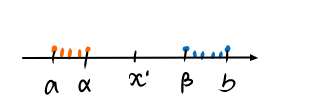
记 在 上振幅为
且仍由于左右至少各1个区间 => 区间长度
(此时理想情况 被分为 )
则
从而 , 故 的分割 (上图橙色); 的分割 (上图蓝色)
使得
令 为 的分割,则
单调→可积
定理 若 在 单调, 则
Analysis
可以足够小:分割足够细即可
绝对值中同号:
Proof
取分割 ,满足
防止则
绝对值中同号
可积→分段可积
定理 设 在 和 可积
Analysis
已知: 分割 ,使
Proof
令 ,则 为 加细分割
令 (取一部分和)
显然
即
略
绝对可积
Proof
由条件:
有
从而
平方可积
乘积可积
设 , 则
复合可积
设 , , 则
Proof
摘自陈纪修版数学分析
由于 在 连续, 所以可设 , 且 一致连续(闭区间有界)
于是 , 只要 , 就成立
由于 在 上可积, 由上题, 对上述 与 , 存在划分 , 使得振幅 的小区间的长度之和小于 ,于是
即复合函数 在 上可积.
闭区间有界+间断点收敛→可积
设 在 有界, 其间断点全体为 , 且 ,则 .
Analysis
上有有限的间断点
只要区间长度短,振幅就不会超过
Proof
由条件在上的振幅上至多个间断点从而的分割使得该区间振幅
例题:Riemann 函数可积
例 证明 Riemann 函数 在 可积
Analysis
设 , 中满足 的有理点 至多有有限个
不妨设有 个,为
对分割 , 记
于是
元素个数Proof
函数值小于 sigma =>振幅一定小于sigma
的子区间含取分割
Proof.2
摘自陈纪修版本数学分析
由 Riemann 函数的性质, 对任意给定的 ,在 上使得 的点至多只有有限个
不妨设是 个,记为 .
作 的划分 , 使得满足
,
.....
,
,
图 7.1.6 表示的是的情况.由于
而在右边的第一个和式中,有且;
在第二个和式中,有且,
因此得到
.
由定理 7.1.3, Riemann函数可积.
证毕
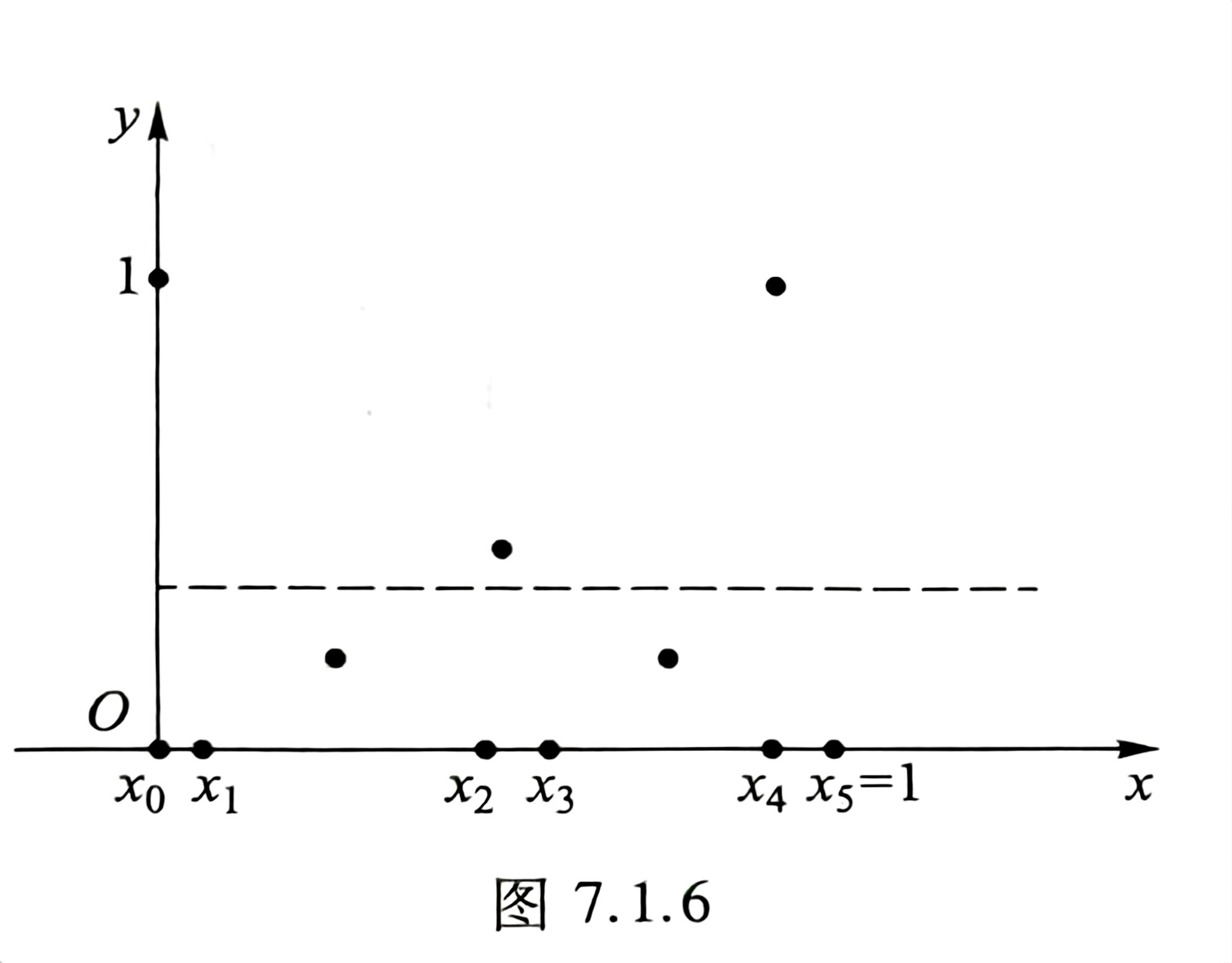
如图为 (有两个点超出)的情况
满足:1. ;2.